You are here
The shape of the Eiffel Tower
I've got interested, since I am going with about 10 of my students to Paris for the Euromech conference I am coorganizing in July, by the design of the Eiffel Tower. Eiffel was a great engineer, and indeed his shape of the tower apparently comes from his ingenious idea of balancing weigth and wind pressure so that there is little need of foundations. WIKIPEDIA has an account of this design idea, and the resulting integro-differential equation.
I added a preprint with permission of the Solution of Eiffel-Chouard equations by Weidman and Pinelis as attachment here, together with actual Excel file of the Eiffel tower profile measurement by Eiffel himself and others.... Have fun!
More infos on the great Engineer Gustave Eiffel for example at http://en.wikipedia.org/wiki/Gustave_Eiffel
Design of the
tower
Material
The metal structure of the Eiffel Tower weighs 7,300 tonnes while the
entire structure, including non-metal components, is approximately
10,000 tonnes. As demonstration of the economy of design, if the 7,300
tonnes of the metal structure were melted down it would fill the 125
metre square base to a depth of only 6 cm (2.36 in), assuming a density
of the metal to be 7.8 tonnes per cubic metre. Depending on the ambient
temperature, the top of the tower may shift away from the sun by up to
18 cm (7.1 in) because of thermal expansion of the metal on the side
facing the sun.
Wind
considerations
At the time the tower was built many people were shocked by its
daring shape. Eiffel was criticised for the design and accused of trying
to create something artistic, or inartistic according to the viewer,
without regard to engineering. Eiffel and his engineers, however, as
experienced bridge builders, understood the importance of wind forces
and knew that if they were going to build the tallest structure in the
world they had to be certain it would withstand the wind. In an
interview reported in the newspaper Le Temps, Eiffel said:
Now to what phenomenon did I give primary concern in designing the
Tower? It was wind resistance. Well
then! I hold that the curvature of the monument's four outer edges,
which is as mathematical calculation dictated it should be [...] will
give a great impression of strength and beauty, for it will reveal to
the eyes of the observer the boldness of the design as a whole.[22]
The shape of the tower was therefore determined by mathematical
calculation involving wind resistance. Several theories of this
mathematical calculation have been proposed over the years, the most
recent is a nonlinear integral differential equation based on
counterbalancing the wind pressure on any point on the tower with the
tension between the construction elements at that point. That shape is
exponential. A careful plot of the tower curvature however, reveals two
different exponentials, the lower section having a stronger resistance
to wind forces.[23][24]
The tower sways 6–7 cm (2–3 in) in the wind.[25]
23^
Translated from the French newspaper Le Temps of 14 February
1887. Extrait de la réponse d'Eiffel
24 ^ Elegant Shape Of Eiffel Tower
Solved Mathematically By University Of Colorado Professor
25 ^ The Virginia Engineer: Correct
Theory Explaining The Eiffel Tower’s Design Revealed
Do you have the original files or PDF? Can you share them with me? Any interest to discuss about this question on imechanica, and/or with my students? Incidentally, my students are invited to comment in particular!!
| Attachment | Size |
|---|---|
| 9.4 MB | |
| 106 KB |
- Mike Ciavarella's blog
- Log in or register to post comments
- 52896 reads


Comments
some of the reports of the new findings
Correct Theory Explaining The Eiffel Tower’s Design Revealed
January 31, 2005
Iosif Pinelis, a professor of mathematical sciences, first became
intrigued by the problem in 2002, when Patrick Weidman, an associate
professor of mechanical engineering at the University of Colorado at
Boulder, visited Michigan Tech (MTU). Prof. Weidman presented two
competing mathematical theories, each purporting to explain the Eiffel
Tower’s elegant design.
One, by Christophe Chouard, argued that Eiffel engineered his tower
so that its weight would counterbalance the force of the wind. According
to the other theory, the wind pressure is counterbalanced by tension
between the elements of the tower itself, Prof. Pinelis said.
Chouard had developed a nonlinear integral equation to support his
theory, but finding its solutions was proving difficult. “Weidman and
the mathematicians whom he had consulted could only find one solution, a
parabola, of the infinitely many solutions that Chouard’s equation must
have,” Prof. Pinelis said. As anyone who has survived high-school
geometry can quickly testify, the Eiffel Tower’s profile doesn’t look
anything like a parabola. Prof. Weidman asked MTU mathematicians if they
could come up with any other solutions.
Prof. Pinelis went back to his office and soon found an answer
confirming Prof. Weidman’s conjecture that Chouard’s theory was wrong.
It turns out that all existing solutions to Chouard’s equation must
either be parabola-like or explode to infinity at the top of tower.
“The Eiffel Tower does not explode to infinity at the top, and its
profile curves inward rather than outward,” Prof. Pinelis notes. “That
pretty much rules out Chouard’s equation.”
Prof. Weidman then went to the historical record, and found an 1885
memoire delivered by Eiffel to the French Civil Engineering Society
affirming that Eiffel had indeed planned to counterbalance wind pressure
with tension between the construction elements.
Using that information, Prof. Weidman and developed an nonlinear
integral-differential equation whose solutions yielded the true shape of
the Eiffel Tower. That shape is exponential.
The work by Prof. Weidman and Prof. Pinelis, “Model Equations for
the Eiffel Tower Profile: Historical Perspective and New Results,” has
appeared in the French journal Comptes Rendus Mecanique, published by
Elsevier and the French Academy of Sciences.
“The funny thing for me was that you didn’t have to go into the
historical investigation to disprove a wrong theory,” Prof. Pinelis
says. “The math confirms the logic behind the design. For me, it was
more fun to go to the math.”
Permanent Link
Michele Ciavarella, Politecnico di BARI - Italy, Rector's delegate.
http://poliba.academia.edu/micheleciavarella
Editor, Italian Science Debate, www.sciencedebate.it
Associate Editor, Ferrari Millechili Journal
Some videos of interest, but distracting from the problem
Stages of construction of the Eiffel Tower
Eiffel Tower Construction view: girders at the first story
Panoramic view during ascension of the Eiffel Tower by the Lumière brothers, 1898
Franz Reichelt's preparations and fall from the Eiffel
Tower.
Lightning strikes the Eiffel Tower on June 3, 1902, at 9:20 P.M.
Adolf Hitler with the Eiffel Tower in the background
Michele Ciavarella, Politecnico di BARI - Italy, Rector's delegate.
http://poliba.academia.edu/micheleciavarella
Editor, Italian Science Debate, www.sciencedebate.it
Associate Editor, Ferrari Millechili Journal
Let's return to the problem: the equation for the shape!
Elegant Shape Of Eiffel Tower Solved
Mathematically By University Of Colorado Professor
ScienceDaily (Jan. 7, 2005) —
An American engineer has produced a mathematical model explaining the
elegant shape of the Eiffel Tower that was derived from French engineer
Gustave Eiffel's writings regarding his own fears about the effects of
wind on such a structure.
University of Colorado at Boulder Associate Professor Patrick Weidman
said Eiffel, one of the premier structural engineers in history, was
determined to build the world's first tower reaching 300 meters, the
nearest metric equivalent to 1,000 feet, into the sky. The tower was
designed to be the centerpiece of the World's Exposition in Paris,
marking the centennial of the French Revolution.
But such a tower, never having been successfully erected, raised a
chronic concern of Eiffel that he expressed frequently in his
communications.
"Eiffel was worried about the wind throughout his building career,"
said Weidman of the CU-Boulder mechanical engineering department.
"Although he was astoundingly bright, he was forced to rely on practical
experience rather than mathematical calculations to estimate the
effects of wind forces on structures."
Weidman said the Eiffel Tower was not designed according to a single,
overarching mathematical formula. Instead, Eiffel's engineers used
graphical results to calculate the strength needed to support its
tremendous weight, as well as empirical evidence to account for the
effects of wind. "He built it section by section, and did not have an
equation for its description," said Weidman.
But the spectacular tower, completed in 1889 and which remains one of
the most romantic and recognizable structures in the world, has long
been believed to be explainable using a mathematical equation, albeit a
very complex one.
Weidman began researching the problem when he received a second
edition copy of the textbook, "Advanced Engineering Mathematics," in
2001. The book's cover contains photographs of various stages of the
Eiffel Tower's construction, and the book's preface contains a
non-nonlinear integral equation -- a formula with a number of possible
solutions -- for the tower's shape.
The equation was created by French Eiffel Tower aficionado Christophe
Chouard, who posted it on his Web site and challenged engineers and
mathematicians worldwide to find its solution, said Weidman. In terms of
known mathematical functions, Weidman found one solution -- a downward
facing parabola, but it has the wrong curvature for the legendary
structure.
After giving a talk at Michigan Technological University in 2003,
Weidman was introduced to Professor Iosif Pinelis, an expert in
mathematical analysis, who offered his help in understanding the
underlying features of the integral equation. Calculations by Pinelis
showed that all existing solutions to Chouard's equation must be either
parabola-like -- which the Eiffel Tower is not -- or "explode to
infinity" at the top of the tower.
Weidman, who said he became obsessed with the problem, began to read
more about the life of Eiffel and his construction efforts. He contacted
Henri Loyette, author of a 1985 book on the life of Eiffel and now the
curator of the Louvre in Paris, who suggested Weidman search the
historical archives.
Weidman tracked down a copy of a communication from Eiffel to the
French Society of Civil Engineers dated March 30, 1885. Written in
French, the document affirmed that Eiffel planned to counterbalance wind
pressure with the tension between the tower's construction elements.
After translating the 26-page document with the help of professional
translator Claudette Roland, Weidman finally deduced the basis for tower
construction. A key factor for Eiffel was determining where the
tangents to the skyline profile -- which run from given horizontal
sections of the tower -- intersect the resulting wind forces acting
above those sections.
"Eiffel discovered this form of construction produces no load in the
diagonal truss elements commonly used to counteract the bending moment,
or torque, of the wind, and hence those truss members could be
eliminated," Weidman said. "This allows for a reduction of the tower
weight and reduces the surface area exposed to the wind."
Based on the information, Weidman derived a new equation for the
skyline profile -- one that "embraces Eiffel's deep concern for the
effects of wind-loading on the tower," he said. Weidman found an exact
solution of the equation in the form of an exponential function that
closely matches the shape of the tower's upper half.
The tower is composed of four arched, wrought-iron legs tapering
inward to form a single column that rises to 300 meters, or 986 feet.
The top level was built with a large room that Eiffel used for
meteorological studies, capped by a spiral staircase and a television
antenna that reaches to 1,052 feet today.
Plotting the actual shape of the tower reveals two separate
exponential sections that are hooked together, he said. Since Eiffel did
not seem confident in estimating the wind torque on the tower, he
"overdesigned" the bottom section, beefing it up for safety reasons.
"The structural factor of safety is responsible for the second
exponential equation describing the lower half of the tower," Weidman
said.
Weidman and Pinelis presented their findings in a paper titled "Model
Equations for the Eiffel Tower Profile: Historical Perspective and New
Results."
The paper appeared in the July 2004 issue of the journal, "Comptes
Rendus Mecanique," published by Elsevier and the French Academy of
Sciences. In addition, the English translation of Eiffel's 1885
communication to the Society of French Engineers by Weidman and Roland
recently was accepted for publication in the Architectural Research
Quarterly published in Great Britain.
"While the events of the French Revolution are captured by Charles
Dickens in his poignant novel, "A Tale of Two Cities," the centennial of
the French Revolution is commemorated by Eiffel's graceful tower, the
skyline profile of which is "A Tail of Two Exponentials," Weidman and
Pinelis wrote in their 2004 paper.
The Eiffel tower, notes Weidman, "is a structural form molded by the
wind." This was Eiffel's point more than a century ago, when he wrote
about the four stout legs supporting the legendary tower: "Before they
meet at such an impressive height, the uprights appear to spring out of
the ground, moulded in a way by the action of the wind itself."
Michele Ciavarella, Politecnico di BARI - Italy, Rector's delegate.
http://poliba.academia.edu/micheleciavarella
Editor, Italian Science Debate, www.sciencedebate.it
Associate Editor, Ferrari Millechili Journal
And here is Chouard Eiffel's equation!
http://www.chouard-eiffel-equation.com/
ntroduction:
Gustave Eiffel was proud of his good-loking Tower whose shape resulted
from
mathematical
calculation, as he
said.
At any height on the Tower, the moment of the weight of the higher
part
of the Tower, up to
the top, is equal to the moment of the strongest wind on this same part.
Writing the differential equation of this equilibrium allows us to
find
the "harmonious equation"
that describes the shape of the Tower.
Writing the equation:
Let A be a point on the edge of the Tower. Let x be the distance
between the top of the Tower and A. Let P(x) be the weight of
the part of the Tower above A, up to the top of the Tower.
Let f(x) be the half-width of the Tower at A. The moment of
the weight of the Tower relative to point A is equal to P(x)·f(x).
Michele Ciavarella, Politecnico di BARI - Italy, Rector's delegate.
http://poliba.academia.edu/micheleciavarella
Editor, Italian Science Debate, www.sciencedebate.it
Associate Editor, Ferrari Millechili Journal
And the resulting equation is
The function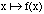
, which gives the width of the Eiffel Tower as a function
of the distance from top, is a solution of the following equation:
How can function f(x) be written as a combination of usual
functions
?
If you can solve this equation, please E-mail me the solution: christophe@chouard.com
This has resulted in many replies including those of the double exponential solution explained above
Michele Ciavarella, Politecnico di BARI - Italy, Rector's delegate.
http://poliba.academia.edu/micheleciavarella
Editor, Italian Science Debate, www.sciencedebate.it
Associate Editor, Ferrari Millechili Journal
Some more impressive images of the Tower and its shape..
Michele Ciavarella, Politecnico di BARI - Italy, Rector's delegate.
http://poliba.academia.edu/micheleciavarella
Editor, Italian Science Debate, www.sciencedebate.it
Associate Editor, Ferrari Millechili Journal
I received a nice email from Christophe Chouard
I've received a number of files from Christophe
Chouardon the Eiffel Tower Equation, and also an Excel file where all
dimensions and angles of the various sections of the Tower are listed. Anyone interested can write to me.
Christophe
Chouard also said that my students can feel free to make any use you want
of the URL of his site:
http://www.chouard-eiffel-equation.com/
He also said "By
the way, I am just an engineer by training who works in finance (!). I
fell in love with the Tower 15 years ago and I have used my souvenirs
of math in order to write the equation, but then I failed to solve it
since my
knowledge in math is limited. I am just glad that this challenge has
triggered some interest from real mathematicians around the globe,
thank-you internet."
So my students and all Imechanicians can have fun if they want
Thanks to Christophe
Chouard!
Michele Ciavarella, Politecnico di BARI - Italy, Rector's delegate.
http://poliba.academia.edu/micheleciavarella
Editor, Italian Science Debate, www.sciencedebate.it
Associate Editor, Ferrari Millechili Journal
I've added some files to the main post which go into details
I've added the actual PDF and excel files which you need to gather all infos in the main post
http://imechanica.org/node/8117
I've noticed a certain similarity with equation of the classical problem of a gear loaded on its tip (usually solved with beam theory, leading to the classical modulus equation by Lewis). But I have to investigate further possible analogies, also because I fail to remember that gear teeth have exponential shape. I will think about it, but obviously the analogy Eiffel tower profile -- gear tooth profile is limited by the fact that gears are usually obtained by cutting and so usually form enveloping curves...
The module system
Countries which have adopted the metric
system generally use the module system. As a result, the term
module is usually understood to mean the pitch diameter in millimeters
divided by the number of teeth. When the module is based upon inch
measurements, it is known as the English module to avoid
confusion with the metric module. Module is a direct dimension, whereas
diametral pitch is an inverse dimension (like "threads per inch"). Thus,
if the pitch diameter of a gear is 40 mm and the number of teeth 20,
the module is 2, which means that there are 2 mm of pitch diameter for
each tooth.[18]
[edit] Manufacture
Gear Cutting simulation (length 1m35s) faster, high bitrate version.
This section requires expansion.
Gear are most commonly produced via hobbing,
but they are also shaped, broached, cast,
and in the case of plastic gears, injection molded. For metal gears the teeth are usually heat treated to make them hard and more wear resistant while leaving the
core soft and tough.
For large gears that are prone to warp a quench
press is used.
Michele Ciavarella, Politecnico di BARI - Italy, Rector's delegate.
http://poliba.academia.edu/micheleciavarella
Editor, Italian Science Debate, www.sciencedebate.it
Associate Editor, Ferrari Millechili Journal, http://imechanica.org/node/7878
The analogy with Lewis formulae however appears
Bending Stresses - The Lewis Formula
Although this was published in
1893, it is still very widely used for assessing
bending stresses when designing gears. The method involves moving the
tangential force and
applying it to the tooth tip and assuming the load is uniformly
distributed accross the
tooth width with the tooth acting as a simple cantilever of constant
rectangular cross
section, the beam depth being put equal to the thickness of the tooth
root (t) and
the beam width being put equal to the tooth, or gear, width (bw).
The
section modulus is I/c = bwt2/6 so the bending
stress is given by:
sigmabending
= M/(I/c) = 6WtL/(bwt2) eqn.1.
Assuming that the
maximum bending stress is at point 'a'.
By
 eqn.2
eqn.2
similar triangles:
or
Rearranging eqn.1 gives:
Substitute the
value for 'x' from eqn.2 and multiply
the numerator and denominator by the circular pitch, 'p' gives:
This
is the original Lewis equation and 'y' is called the
Lewis form factor which may be determined graphically or by computation.
Engineers often now work with the 'diametral pitch', 'P',
 and
and  or the 'module', 'm', which is 1/diametral pitch
or the 'module', 'm', which is 1/diametral pitch
= 1/P
Then where
where
Y = 2xP/3
Written in terms of the module:
sigmabending = Wt/(bwmY)
The Lewis form
factor considers only static loading, it is dimensionless,
independent of tooth size and is a only a function of tooth shape. It
does not take into
account the stress concentration that exists in the tooth fillet.
(from http://www.tech.plym.ac.uk/sme/desnotes/gears/desgear1.htm)
This is all interesting... but needs thinking... any suggestions from imechanicians?
Michele Ciavarella, Politecnico di BARI - Italy, Rector's delegate.
http://poliba.academia.edu/micheleciavarella
Editor, Italian Science Debate, www.sciencedebate.it
Associate Editor, Ferrari Millechili Journal, http://imechanica.org/node/7878